Parametric regression is a mathematical model of a phenomenon in the form of functional dependence between the parameters of this phenomenon, one of which is a dependent variable and independent arguments of a function, and the other is its unknown estimated parameters.
Since measurements are often burdened with errors, the construction of the model is carried out in the probabilistic scheme of the problem statement, and the estimates of unknown parameters are carried out by statistical methods using evaluation equations. For a nonlinear regression that is not intrinsically linear, the estimated equations with respect to the estimated parameter are not analytically solved. In this case, iteration methods are used, the effectiveness of which depends on the initial approximation. There is an iterative formula for generalized minimal-contrast estimation of non-linear one-parameter pair (one argument) regression. Its components are the implementations of the estimated regression parameter found analytically or numerically by the regression function at measured values of the dependent variable and the independent argument without taking into account the measurement errors. The average of these realizations with a certain approximation accuracy is a consistent estimate, which was previously proved by the numerical characteristics of the realizations found. This estimate can be used as an initial estimate in an iterative parametric regression estimation formula.
In this paper, the implementation of the estimated parameter with approximately zero variance is considered not only as an initial approximation, but also as a self-sufficient estimate, if its accuracy is satisfactory. It is an approximation of the estimated parameter of known accuracy proportional to the cube of the standard deviation of the initial data.
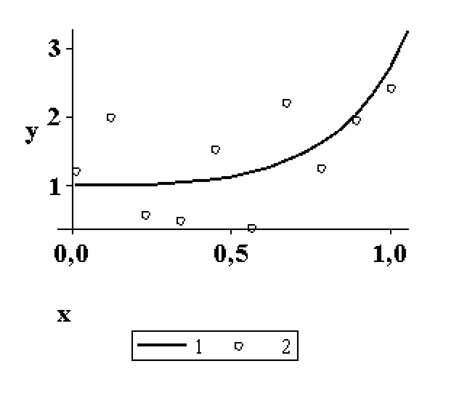
The results of the simulation experiment for estimating regression parameters by the proposed approximation method and by means of a consistent assessment are consistent with the theoretical descriptions of the methods. Their comparison is in favor of approximation, if the volume of the original data is less than ten. In this case, the deviation from the true value of the estimated parameter is less than the deviation of the compared state estimate by a maximum of two orders of magnitude (188 times) by at least 1.5 times.
Conditions of optimality of the method assumes its use in studies of rare phenomena, as well as in expensive experiments in the broad (economic and humanitarian) sense of the word,
The effectiveness of the evaluation method can be anticipated by checking to experience the fulfillment of the conditions of evaluation formation, which depend on the range of values of the argument of the regression function.